만유인력의 법칙
- 질량을 가지 두 물체는 인력이 작용
– 물체 질량의 곱에 비례
– 거리 제곱에 반비례 - 중력 (Gravity)
- 중력 (나무위키)
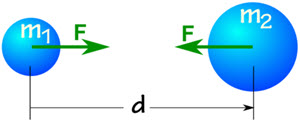
\huge{ F = G \frac{m1 m2}{d^2} }
- G는 중력상수(실험적으로 측정) = 6.674×10-11 N m2/kg2
- 지구표면의 중력 = 9.8 m/s2
– 사과(질량) 0.1kg 이 갖는 힘은 ?
F = ma
F = mg
F = 0.1 kg × 9.8 m/s2
F = 0.98 kg m/s2
F = 0.98 N
=> 약 1 뉴튼(N)
지구와 달
GlowScript 2.9 VPython
# 지구 : 반지름 6,400,000m, 6,400km
Earth = sphere(pos = vector(0,0,0), radius = 6400000, texture = textures.earth)
# 달 : 지구와 거리 385,000,000m 385,000km, 반지름 1,737,000m 1,737km
Moon = sphere(pos = vector(385000e3,0,0), radius = 1737000, make_trail = True)
sf = 6 #scailing factor
Earth.radius = sf*Earth.radius
Moon.radius = sf*Moon.radius
# 중력상수, 만유인력상수, 뉴턴상수: 6.674×10-11 N m2/kg2
G = 6.67e-11
# 지구 질량
Earth.mass = 5.972e24
# 달 질량
Moon.mass = 7.347e22
Earth.v = vec(0,0,0)
Moon.v = vec(0,0,0)
# time
t = 0
dt = 60
# Simulation Loop
while True:
rate(1000)
# Forces
r = Earth.pos - Moon.pos
Moon.f = G * Earth.mass * Moon.mass / mag(r) ** 2 * norm(r)
Earth.f = -Moon.f
# Time Integration
Moon.v = Moon.v + Moon.f/Moon.mass*dt
Earth.v = Earth.v + Earth.f/Earth.mass*dt
Moon.pos = Moon.pos + Moon.v*dt
Earth.pos = Earth.pos + Earth.v*dt
t = t + dt
# Collision Check
if Earth.radius + Moon.radius > mag(r):
print("Collision!")
print(t/60/60/24, "days")
break
달의 공전
- 달의 공전속도 = 1,022km/s
– Moon.v = vec(0, 1022, 0) - 코드 05-01
– 만유인력에 의해 (서로 끌어당겨) 점점 위로 올라감
– 지구의 초기속도를 달의 초기속도 반대 방향으로 설정
– 지구의 초기속도 = 달의 속도 x 달의 질량 / 지구의 질량
Earth.v = -Moon.v * Moon.mass / Earth.mass
-> 운동량 보존의 법칙 : 지구와 달을 하나의 시스템을 보았을때 운동량을 0으로 만드는 방법 (이렇게 하면 질량 중심의 위치가 변하지 않음) - 코드 05-02
- 공전속도를 반으로 해보면…
– Moon.v = 0.5*Moon.v
– 지구와 가까워졌을때 빨라짐 => 케플러 법칙에 정확히 부합 - 달의 공전속도를 1.2배로 해보면?
– Moon.v = 1.2*Moon.v
– 1.5배로 하면 멀리 가버림. 지구 중력이 달을 끌어당기지 못함. => 탈출속력
– 탈출속력 : 지구의 중력을 이기고 탈출할 정도의 속력
3체운동
- 세 물체가 받는 만유인력을 다 계산
- 코드 5-04
– 위성 위치를 중심에
– 질량은 지구질량의 1/10 : sat.m = 1/10*earth.m
– 지구와 달의 질량이 같으면 평형 운동 - 코드 05-04-1 : 위성의 위치를 아주 약간 지구쪽으로 이동 : vector(-0.01*r,0,0)
- 코드 05-04-2 : 더 작게 이동 : vector(-0.001*r,0,0)
- 수학적 계산으로는 예측할 수 없고 컴퓨터 계산으로 근사적인 형태만 알 수 있음.
탐사선을 달로
- 탐사선 질량 15,000 kg
- 지구 반지름에서 10배 떨어진 곳에서 출발
- 연료 없이 지구와 달의 인력으로만 이동
#craft
craft = sphere(pos=vec(-10*Earth.radius, 0,0), radius=1e6, color=color.yellow, make_trail=True)
craft.m = 15e3
- 코드 05-05
– 초속 2km 속도 : craft.v = vec(0,2e3,0) # initial vel without moon
– 지구를 못 벗어남. - 코드 05-05-1
– 초속 3.5km : craft.v = vec(0,3.5e3,0) # hyperbolic
– 멀리 가버림. - 코드 05-05-2
– #craft.v = vec(0,3.3e3,0) : 달의 뒷면 탐사
– #craft.v = vec(0,3.27e3,0) #critical pt : 달의 앞면 탐사.
– 물고기 모양 괘도
시뮬레이션
- 수학적 일반해를 가지지 못하는 3체운동의 움직임을 확신할 수 있는 이유?
– 시간 간격을 줄여 시뮬레이션을 진행해도 퀘도가 크게 달라지지 않음을 확인
– 시뮬레이션을 통해 근사해를 구함
