축구공이 받는 힘
중력

- (계산한) 지구표면의 중력의 힘 : 9.8 m/s2

g = -9.8 #m/s**2
# Gravity Force
grav = ball.m * vec(0,g,0) #gravity
공기저항력
- 공기에 의한 저항
– 물체가 기체 분자와 부딪히면서 (물체의 운동방향)속도 반대 방향으로 작용


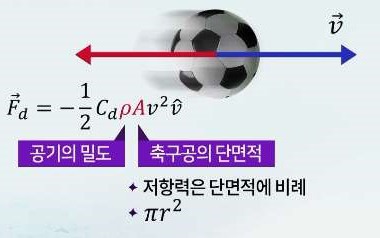

축구공이 받는 힘
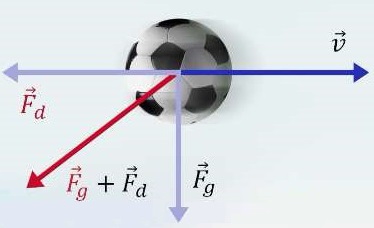
프리킥 시뮬레이션
프리킥 코드 06-01
GlowScript 2.9 VPython
# ground 운동장
ground = box(pos=vec(0,0,0),size=vec(100,0.10,70), color = color.green)
# init. positon & velocity of ball
init_pos = vec(-30,0.11,0)
ball = sphere(pos=init_pos,radius=0.11, color = color.orange) # m
ball.m = 0.45 # kg
ball.speed = 25 # m/s
ball.angle = radians(35) # c.f) degrees 각도, 35도, 라디안으로 변환
ball.v = ball.speed*vec(cos(ball.angle),sin(ball.angle),0)
attach_trail(ball)
attach_arrow(ball, "v", shaftwidth = 0.1, scale = 0.3, color=color.yellow) # scale : 크기를 30%로 줄여서
# graph
gball_x = gcurve()
scene.range = 30 # x축 간격으로 약 30정도 세팅. 한눈에 들어오게
# const.
g = -9.8 # 중력가속도 m/s**2
rho = 1.204 # 공기의밀도 kg/m**3
Cd = 0.3 # laminar 저항계수
#time setting
t = 0
dt = 0.01
while t < 20:
rate(1/dt)
# Gravity Force
grav = ball.m * vec(0,g,0)
# Drag Force
drag = -0.5*rho*Cd*(pi*ball.radius**2)*mag(ball.v)**2*norm(ball.v)
print("gravity: ", mag(grav), 'drag force: ',mag(drag))
# Sum of Forces
ball.f = grav + drag
# Time stepping
ball.v = ball.v + ball.f/ball.m*dt
ball.pos = ball.pos + ball.v*dt
# graph
gball_x.plot(pos=(t,mag(init_pos - ball.pos)))
# collision
if ball.pos.y - ball.radius < 0:
#print(ball.pos.x)
break
t = t + dt
공기저항력없는 프리킥 코드 06-02
# Sum of Forces
ball.f = grav + drag
ball2.f = grav
바람이 불때 프리킥 코드 06-03
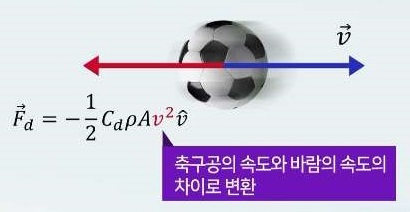 # wind
wind_speed = 5 # m/s
#wind_speed = -5 # m/s
#wind_speed = -10 # m/s
wind_v = wind_speed*vec(1,0,0)
# Drag Force
ball.v_w = ball.v - wind_v
drag_wind = -0.5*rho*Cd*(pi*ball.radius**2)*mag(ball.v_w)**2*norm(ball.v_w)
# Sum of Forces
ball.f = grav + drag_wind
# wind
wind_speed = 5 # m/s
#wind_speed = -5 # m/s
#wind_speed = -10 # m/s
wind_v = wind_speed*vec(1,0,0)
# Drag Force
ball.v_w = ball.v - wind_v
drag_wind = -0.5*rho*Cd*(pi*ball.radius**2)*mag(ball.v_w)**2*norm(ball.v_w)
# Sum of Forces
ball.f = grav + drag_wind
마그누스 효과
- 공에 회전
– 회전하는 방향으로 공이 휨
– 마그누스 힘, 마그누스 효과
– 물체주변의 공기 + 물체 회전
– 진공에서는 휘지 않음.
– 물체와 기체분자와의 상호작용
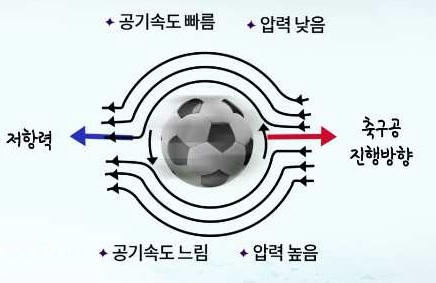
– 기체분자가 축구공에 미치는 알짜힘 ->위쪽 방향으로의 힘.










바나나킥 시뮬레이션 08-01
Cm = 1 # 저항계수
w = 10*2*pi # 10 rev. per sec 초당 10회전
# Magnus Force
magnus = 0.5*rho*Cm*(pi*ball.radius**2)*ball.radius*w*mag(ball.v)*cross(vec(0,1,0),norm(ball.v))
# Sum of Forces
ball.f = grav + drag + magnus
바나나킥 시뮬레이션 (슬라이더 UI) 08-02
## UI
scene.append_to_caption(' \nInitial Values \n \n')
# slider
velocitySlider = slider(min = 0, max = 45, value = 25, bind = setVelocity)
scene.append_to_caption(' \nVelocity:',velocitySlider.min, 'to' ,velocitySlider.max, '\n \n')
def setVelocity():
global ball
ball.speed = velocitySlider.value
ball.v = ball.speed*vec(cos(ball.angle),sin(ball.angle),0)







 # wind
wind_speed = 5 # m/s
#wind_speed = -5 # m/s
#wind_speed = -10 # m/s
wind_v = wind_speed*vec(1,0,0)
# Drag Force
ball.v_w = ball.v - wind_v
drag_wind = -0.5*rho*Cd*(pi*ball.radius**2)*mag(ball.v_w)**2*norm(ball.v_w)
# Sum of Forces
ball.f = grav + drag_wind
# wind
wind_speed = 5 # m/s
#wind_speed = -5 # m/s
#wind_speed = -10 # m/s
wind_v = wind_speed*vec(1,0,0)
# Drag Force
ball.v_w = ball.v - wind_v
drag_wind = -0.5*rho*Cd*(pi*ball.radius**2)*mag(ball.v_w)**2*norm(ball.v_w)
# Sum of Forces
ball.f = grav + drag_wind